Résumé

Ce mois-ci, nous allons utiliser les primitives graphiques d'OpenScheme pour écrire une bibliothèque permettant d'afficher des graphes. Nous constaterons la grande souplesse de ce langage pour manipuler des structures de données dynamiques. Le code présenté est un prétexte pour programmer en Scheme avec un objectif assez ludique, puisque ayant trait au graphisme. Le programme présenté utilise beaucoup de techniques que l'on retrouve en Scheme.

Le programme présenté dans cet article est disponible sur le site http://www.open-scheme.com/pub/graph.osm.

L'environnement OpenScheme est toujours disponible sur http://www.open-scheme.com et sur le CDROM du magazine. La version actuelle est 1.3.3, pour les plateformes Intel sous Linux, Windows, FreeBSD, Solaris et BeOS. Le port sur plateformes Sparc est en cours.

Cet environnement existe en version libre ou commerciale. Nous rappelons que le tutoriel d'OpenScheme disponible sur le site WEB rassemble les articles précédents parus dans Linux Magazine.

Introduction

La bibliothèque graphique d'OpenScheme est un ensemble de fonctions primitives gérant l'affichage graphique. Cette bibliothèque de fonction est disponible de manière identique pour les environnements issus d'Unix et Windows. Le même programme tournera de manière identique sur tous les systèmes d'exploitation supportés par OpenScheme.

Les lecteurs souhaitant programmer avec OpenScheme auront intérêt à utiliser la version de débogage de l'environnement, permettant de visualiser les variables, de poser des points d'arrêts et de visiter la pile des appels de fonctions. Nous rappelons qu'OpenScheme est le seul environnement Scheme proposant un débogage au niveau expressions.

Le programme que nous décrivons ici est un cas pratique d'utilisation du langage. Le grapheur est un logiciel permettant de tracer des courbes dans une fenêtre en donnant un ou plusieurs producteurs qui sont des fonctions numériques. Le grapheur proposé ici est très simple et ne propose qu'un nombre limité d'options. Voici un exemple d'utilisation du grapheur :

Osm> (graph ; mode de tracé = dot ou line
'line
; x initial
0
; x final
(* 2 3.14116)
; pas pour x
0.1
; producteurs
sin cos)

=> #unspecified

La fonction graph possède comme premier paramètre le type de tracé souhaité ; le choix est soit le symbole dot pour un tracé en point à point, soit line pour un tracé en ligne. D'autres modes de tracé peuvent être ajoutés, comme le tracé en rectangles ou en camembert. Ensuite, on spécifie la page des valeurs de x en donnant la valeur initiale, la valeur finale et le pas. Ces valeurs peuvent être positives, négatives, entières ou réelles. Les producteurs sont invoqués pour les différentes valeurs de x appartenant à la plage définie. Le nombre de producteur est quelconque. Un producteur est une fonction ayant comme argument une valeur de x, et retournant la valeur de y correspondante. La fonction peut être aussi complexe que nécessaire.

Dans l'exemple, les producteurs sont les fonctions standards sin (sinus) et cos (cosinus) de Scheme. La fenêtre affichée par le grapheur est la suivante :

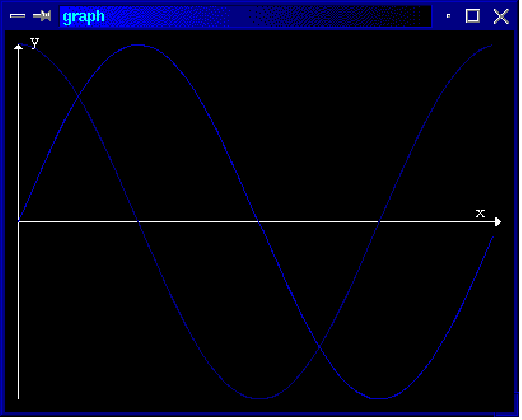
Figure 1 : graphe des fonctions sinus et cosinus entre 0 et 2.pi.

Pour tracer une fonction d'équation y=x, nous invoquons la fonction graph comme cela :

Osm> (graph ; mode de tracé = dot ou line
'line
; x initial
0
; x final
(* 2 3.14116)
; pas pour x
0.1
; producteurs
(lambda (x) x))

=> #unspecified

Nous pouvons combiner toutes sortes de fonctions, à la seule condition que le producteur soit une fonction à 1 argument retournant une valeur numérique. Si nous voulons tracer la fonction f(x)=3.x²+5.x-3, nous appelons graph avec comme producteur la fonction :

Osm> (graph ; mode de tracé = dot ou line
'line
; x initial
0
; x final
(* 2 3.14116)
; pas pour x
0.1
; producteurs
(lambda (x)
(+ (* 3 x x)
(* 5 x)
-3)))

=> #unspecified

Réalisation

La réalisation du grapheur tient en 150 lignes de code Scheme faisant appel à la bibliothèque OK présentée dans les deux numéros précédents de Linux Magazine. Nous avons en premier quelques fonctions utilitaires, puis la fonction get-values qui invoque un producteur pour fournir un vecteur de fonction, puis la fonction de tracé plot et enfin la fonction principale graph.

number->integer

Nous définissons tout d'abord une fonction retournant un entier pour toute valeur numérique rationnelle ou réelle passée en argument :

; retourne un entier à partir d'un
; rationnel ou d'un réel
(define (number->integer x)
(cond [(integer? x) x]
[(rational? x) (quotient (numerator x)
(denominator x))]
[(real? x) (inexact->exact x)]
[(complex? x) (error "cannot convert complex")]
[else (error "cannot be converted '~a'" x)]))

Cette fonction sera utilisée pour convertir les valeurs réelles et rationnelles en entiers, seul type accepté par les primitives graphiques. C'est une fonction par cas sur les types de valeurs numériques traitées. On remarquera la fonction error qui prend comme premier argument une chaine de caractères ayant des 'emplacements ~a' qui seront remplacés par l'affichage des arguments suivants.

En Scheme, les calculs sont effectués dans le mode 'le plus exact possible'. Cela signifie que si on divise 1 par 2, Scheme retourne le nombre rationnel 1/2. Ainsi, si on multiplie (1/2)*2, on obtient 1, qui est le résultat exact. Dans le cadre de ce programme, nous allons effectuer des calculs de conversion entre données numériques et coordonnées écran ; pour cela, la division va être utilisée, et Scheme va produire des nombres rationnels. Nous devrons donc utiliser number->integer pour convertir ces nombres rationnels en entier, seul type accepté par les primitives graphiques d'OpenScheme.

get-values

Nous définissons ensuite la fonction qui est chargée de produire un vecteur de valeur à partir de la plage x souhaitée et un producteur. La fonction est définie par :

; retourne un vecteur de n valeurs
(define (get-values min-x max-x step producer)
(check (procedure? producer))
(let* ([n (+ (number->integer
(/ (- max-x min-x) step))
1)]
[values (make-vector n)])
(do ([x min-x (+ x step)]
[i 0 (+ i 1)])
((eq? i n))
(vector-set! values i (producer x)))
values))))

La fonction vérifie tout d'abord que l'argument procucer est une procédure avec l'appel à check. Check est une forme spéciale d'OpenScheme qui permet de placer des vérifications dans les programmes. Ces vérifications peuvent être désactivées lorsque l'on exécute le programme avec un OpenScheme optimisé pour la vitesse : dans ce cas, aucune vérification n'est effectuée, procurant une vitesse d'exécution optimale. Ce mode de fonctionnement ne doit cependant être utilisé qu'avec des programmes surs en bien testé. Cette fonction est l'équivalent Scheme de la macro assert du langage C.

La fonction construit ensuite un vecteur dont la taille est déduite de la plage définie. Ce vecteur est rempli avec les valeurs produites par le producteur, invoqué pour toutes les valeurs de la plage. Ce vecteur est enfin retourné à l'appelant.

min-max

Pour placer automatiquement les axes de notre graphe, nous avons besoin d'une fonction retournant la valeur minimum et la valeur maximum du vecteur de valeurs produit par la fonction précédente. Cette fonction est définie par :

; retourne la paire formée du minium et du maximum
; parmi un vecteur de valeurs
(define (min-max values)
(let ([n (vector-length values)])
(let loop ([i 1]
[min-y (vector-ref values 0)]
[max-y (vector-ref values 0)])
(if (eq? i n)
(cons min-y max-y)
(loop (+ i 1)
(min min-y (vector-ref values i))
(max max-y (vector-ref values i)))))))

Elle est principalement bâtie autour d'une itération construite avec un let nommé (loop). Loop devient une fonction récursive dont les paramètres sont i, min-x et max-y, initialisés avec les expressions 1 et les vector-ref. L'itération se poursuit tant que la valeur i n'est pas égale à n, avec de nouvelles valeurs pour les paramètres de loop. Lorsque la condition d'arrêt est rencontrée, on retourne simplement la paire formée de la valeur minimum et de la valeur maximum trouvée.

Cette forme d'itération utilisant le let nommé est très puissante car complètement paramétrable. Cependant, lorsqu'on le pourra, on préférera utiliser des formes plus classiques comme for-each ou do.

get-plot-color

Pour tracer les courbes en couleur et afin de simplifier le paramétrage du logiciel, nous proposons d'utiliser une fonction retournant une couleur parmi un ensemble prédéfini, de manière cyclique. Cette fonction est réalisée de la manière suivante :

; retourne à chaque appel une couleur
; différente
(define get-plot-color
(let* ([pool (list ok:red
ok:yellow
ok:green
ok:blue)]
[current pool])
(lambda ()
(let ([color (car current)])
(set! current (cdr current))
(if (null? current)
(set! current pool))
color))))

L'aspect remarquable de cette définition est le let* placé 'avant' le lambda : cette écriture permet de définir des variables globales qui ne seront accessibles que dans le corps de la fonction. Ces variables sont pool, initialisée avec une liste de couleurs, et current prenant la même valeur que pool. L'utilisation du let* permet d'initialiser current avec pool. Si nous avions utilisé un simple let, la variable pool aurait été 'invisible' à l'expression initialisant current.

Ainsi, la 'vraie' fonction est le lambda ; la valeur de pool est de current sont conservées entre chaque appel à get-plot-color. Le corps de la fonction prend une couleur de la liste current et déplace current vers l'élément suivant. Si current devient la liste vide, alors elle est initialisée à la valeur de pool, c'est à dire la liste des couleurs.

Ce qui est remarquable avec le langage Scheme, c'est la concision avec laquelle les programmes sont exprimés. Tout ce que l'on 'fait' en Scheme, on peut le faire avec d'autres langages, mais on le fait de manière plus concise en Scheme.

plot

Pour l'instant, nous ne définissons pas la fonction de tracé. Nous définirons cette fonction plus bas. Pour l'instant, nous avons :

(define (plot mode
device
min-x max-x
min-y max-y
list-of-values)
(ok:draw-text device 10 10 "à finir !"))

Les arguments de la fonction sont le mode de tracé défini par le symbole dot ou line, le device où dessiner le graphe, la valeur minimum et la valeur maximum de x, la valeur minimum et la valeur maximum de y et une liste de vecteurs contenant les valeurs y des points à dessiner, vecteurs retournés par la fonction get-values, vue plus haut.

Nous écrivons un petit message en attendant de faire mieux !

create-device

La fonction create-device crée une fenêtre et l'initialise :

; crée et initialise la fenêtre de dessin
(define (create-device proc)
(let ([win (ok:create-window #f
ok:black
600
10
400
300)])
; titre de la fenêtre
(ok:title! win "graph")
; fonction de rappel lorqu'une touche
; est relâchée
(ok:release-callback! win
(lambda (key)
#f))
; fonction de rappel pour l'affichage
(ok:refresh-callback! win
(lambda ()
(proc win)))
; la fenêtre est rendue visible
(ok:show device ok:show:normal))
; boucle des messages
(ok:exec)))

La fonction a comme paramètre une fonction proc destinée à dessiner le graphe dans la fenêtre lorsqu'on l'invoque avec un device. Elle crée une fenêtre et positionne la fonction de rafraîchissement et la fonction appelée lorsque qu'une touche est relâchée sur la fenêtre. Cette dernière fonction de rappel retourne la valeur #f, ce qui a pour effet de stopper le traitement des messages, et donc de quitter le programme.

La fonction rend ensuite la fenêtre visible et entre dans la boucle de traitement des messages.

graph

La fonction principale du programme est graph définie par :

; fonction principale du grapheur
(define (graph mode min-x max-x step . producers)
; vérification des arguments
(check (number? min-x))
(check (number? max-x))
(check (number? step))
(check (< min-x max-x))
(check (not (zero? step)))
(let loop (; itération sur les producteurs
[producers producers]
; les courbes produites
[waves '()]
; min de toutes les courbes
[waves-min-y 0]
; max de toutes les courbes
[waves-max-y 0])
(if (null? producers)
; crée le device avec la fonction de tracé
; boucle sur les messages du gestionnaire
(create-device
(lambda (device)
(plot mode
device
min-x max-x
waves-min-y waves-max-y
waves)))
; produit et collectionne les courbes ;
; calcule aussi le max et le min des y
(let* (; vecteur des valeurs
[values (get-values
min-x max-x step
(car producers))]
; minimum et maximum
[min-max-y (min-max values)]
[min-y (car min-max-y)]
[max-y (cdr min-max-y)])
(loop (cdr producers)
(cons values waves)
(if (null? waves)
min-y
(min waves-min-y min-y))
(if (null? waves)
max-y
(max waves-max-y max-y)))))))

La fonction est organisée autour d'une itération sur les producteurs. Après avoir vérifié la nature des arguments, la fonction entre dans une boucle sur les producteurs en collectionnant la valeur minimale et la valeur maximale de y ainsi que les vecteurs de points produits par les producteurs. Lorsqu'il n'y a plus de producteur, un device d'affichage est créé, avec une fonction anonyme pour l'affichage. Cette fonction fait simplement appel à plot pour afficher les courbes. La création du device entre dans la boucle de gestion des messages ; on ne sort que lorsque la fenêtre est détruite ou que l'on relâche une touche sur la fenêtre.

Le fait intéressant à remarquer dans cette fonction est la construction avantageuse de la fonction d'affichage qui 'capture' les variables dont elle a besoin. L'écriture Scheme semble naturelle est compréhensible, alors que très peu de langages de programmation permettent d'écrire ce genre de choses. Nous sommes bien en présence d'un langage avancé !

La concision du code facilite la mise au point des programmes et leur maintenance, ce qui est directement lié à la rentabilité.

Il nous reste maintenant la fonction de dessin, qui seule va permettre d'afficher les courbes.

plot

La fonction de tracé permet d'afficher les courbes dans le device. Pour le moment, deux modes de tracé sont définis : le mode point à point et le mode ligne. La fonction est définie par :

; fonction de tracé
(define (plot mode
device
min-x max-x
min-y max-y
list-of-values)
(let* (; marge autour de la zone d'affichage
[marge 10]
; nombre de point
[n (vector-length (car list-of-values))]
; dimensions de la fenêtre
; vecteur #(x y largeur hauteur)
[rect (ok:rectangle device)]
; largeur de la fenêtre
[dev-w (- (vector-ref rect 2) marge marge)]
; hauteur de la fenêtre
[dev-h (- (vector-ref rect 3) marge marge)]
; ratio pour x et pour y
[%x (/ dev-w n)]
[%y (/ dev-h (- min-y max-y))]
; position des axes x et y
[xpos (+ marge
(number->integer
(/ (* dev-w min-x)
(- min-x max-x))))]
[ypos (+ marge
(number->integer
(/ (* dev-h max-y)
(- max-y min-y))))]
; convertisseur (x,y) en coordonnées écran
[conv (lambda (x y)
(cons (number->integer
(+ marge (* (- x min-x) %x)))
(number->integer
(* y %y))))])
; couleur des axes et réinit de l'origine
(ok:foreground! device ok:white)
(ok:origin! device 0 0)
; axe des y
(ok:draw-arrow device
xpos (+ dev-h marge)
0 (- dev-h)
5 4 0)
(ok:draw-text device
(+ xpos marge) (+ marge 5)
"y")
; déplacement de l'origine
(ok:origin! device 0 ypos)
; axe des x
(ok:draw-arrow device
marge 0
dev-w 0
5 4 0)
(ok:draw-text device
(- dev-w marge) 0
"x")
; pour toutes courbes...
(for-each
(lambda (values)
; obtenir et régler la couleur
(ok:foreground! device (get-plot-color))
(case mode
[(dot) ; mode point à point
(do ([i 0 (+ i 1)])
((>= i n))
(let ([dot (conv i (vector-ref values i))])
(ok:draw-point device
(car dot)
(cdr dot))))]
[(line) ; mode ligne
(let loop ([i 0]
[last #f])
(if (< i n)
(let ([dot (conv i (vector-ref values i))])
(if last
(ok:draw-line device
(car last)
(cdr last)
(- (car dot) (car last))
(- (cdr dot) (cdr last))))
(loop (+ i 1) dot))))]))
list-of-values)))

La fonction obtient tout d'abord les dimensions de la fenêtre puis calcule les ratios permettant de convertir les valeurs (x,y) en coordonnées écran. La position des axes x et y est calculée, puis une fonction de conversion conv est définie ; cette fonction prend un couple x et y et retourne une paire de coordonnées écran. Elle trace ensuite les axes x et y, puis en fonction du mode de tracé désiré, elle effectue le tracé de toutes les courbes. Les courbes sont tracées en mode point à point, pour chaque valeur de point, un point est dessiné à la position écran correspondante. En mode ligne, le point précédent est nécessaire pour tracer une ligne entre lui et le point actuel.

Améliorations possibles

Le programme présenté ici tient en 150 lignes de code. Il permet le tracé de toutes sortes de courbes en mode point à point ou en mode ligne. De nombreuses améliorations sont possibles comme :

ï‚· paramétrage: le paramétrage du tracé devrait permettre de contrôler les couleurs des courbes, d'ajouter une légende ;

ï‚· Controle des limites : Les valeurs numériques des coordonées de OK sont limitées à seize bits ; or les différents peuvent produire des valeurs sans limites provoquant des affichages étranges. Il serait souhaitable d'ajouter un contrôle des limites ;

ï‚· règle : les axes devraient être tracés avec une règle permettant de voir l'échelle du tracé ;

ï‚· double buffer : dans le programme présenté, le tracé est effectué directement à l'écran ; il serait judicieux de proposer un affichage en double buffer, d'autant plus qu'OpenScheme possède toutes les fonctions nécessaires ;

ï‚· mode de tracé : d'autres modes de tracé devraient être proposés, comme le tracé de camembert ou le tracé en rectangle ;

ï‚· tracé 3D : il serait possible de définir sur la base présentée ici un grapheur en 3D.

Les auteurs

Guilhem de Wailly, directeur de la société Erian Concept : support, formations, configurations, administration, développements Linux. Environnement OpenScheme.

http://www.erian-concept.com

Fernand Boéri, Professeur à l'Université de Nice - Sophia-Antipolis, membre de l'unité SPORTS du laboratoire I3S, spécialiste en modélisation, évaluation de performances et architectures parallèles.

http://www.i3s.unice.fr

Références

Scheme

 Structure et Interprétation des programmes informatiques
H. Abelson, GJ. Sussman
InterEdition

 The Scheme Programming Languages - Ansi Scheme
R. Kent Dybvig
Prentice Hall

 Les langages Lisps - Christian Queinnec
InterEdition

 Programmer avec Scheme - J. Chazarin
Thomson Publishing

 Revised4 Report on the Algorithmic Language Scheme
W. Clinger, J. Rees
ftp://ftp.nj.nec.com/pub/kelsey

Environnements Scheme

 Scm - A. Jaffer
http://www-swiss.ai.mit.edu/~jaffer
La référence des interprètes Scheme. Très petit, rapide, pour beaucoup de plates-formes, extensible.

 PCScheme - Texas Instrument
ftp://cui.unige.ch/public/pcs/pcscheme.exe
Un très bon environnement de programmation Scheme pour DOS, avec éditeur intégré.

 DrScheme - Rice University
http://www.cs.rice.edu/CS/PLT/
Environnement Scheme libre très avancé.

 ChezScheme - Cadence, Inc
http://www.scheme.com/
Environnement Scheme très performant.

 Inlab Scheme - Inlab Software GmbH
http://www.munich.net/inlab/scheme/
Environnement commercial

 EdScheme, 3Dscheme - Scheme, Inc
http://www.schemers.com/
Environnement de programmation Scheme pour Windows.

 OpenScheme - Erian Concept
http://www.open-scheme.com
Environnement professionnel de programmation Scheme comprenant un interprète, un compilateur et un débogueur symbolique.
Existe en version libre et commerciale, pour Linux, FreeBSD, Solaris, Windows et BeOS, sur systèmes Intel.